Trí Trung Nguyễn(Fan Cuồng Doraemon)
|
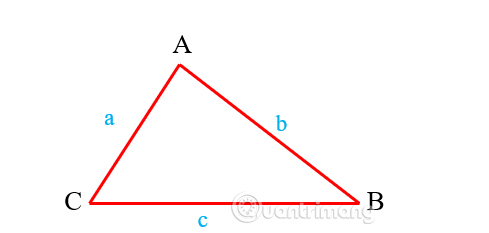
1. Tính chu vi tam giác thường Tam giác thường là tam giác cơ bản có 3 cạnh với độ dài khác nhau. Công thức tính chu vi hình tam giác thường: P = a + b + c Trong đó:
Để tính diện tích nửa chu vi tam giác sẽ dựa theo công thức: ½P = (a+b+c) : 2 Ví dụ: Cho tam giác có độ dài 3 cạnh lần lượt là 4cm, 8cm và 9cm. Tính chu vi hình tam giác. Dựa vào công thức chúng ta sẽ có lời giải là P = 4 + 8 + 9 = 21cm
Tam giác cân là tam giác có 2 cạnh và 2 góc bằng nhau. Đỉnh của tam giác cân là giao diện của 2 cạnh bên. Để tính chu vi tam giác cân, bạn cần biết đỉnh của tam giác cân và độ dài 2 cạnh là được. Công thức tính chu vi hình tam giác cân là: P = 2a + c Trong đó:
Lưu ý, công thức tính chu vi tam giác cân sẽ được áp dụng để tính chu vi của tam giác vuông cân. Ví dụ: Cho hình tam giác cân tại A với chiều dài AB = 7cm, BC = 5cm. Tính chu vi hình tam giác cân. Dựa vào công thức tính chu vi tam giác cân, ta có cách tính P = 7 + 7 + 5 = 19cm.
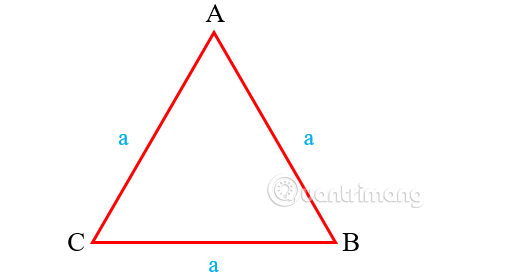
Tam giác đều là trường hợp đặc biệt của tam giác cân khi 3 cạnh bằng nhau. Công thức tính tam giác đều là: P = 3 x a Trong đó
Ví dụ: Tính chu vi tam giác đều có cạnh AB = 5cm. Dựa theo công thức chúng ta có cách tính P = 5 x 3 = 15cm.
Tam giác vuông là tam giác có 1 góc vuông 90°. Công thức tính chu vi tam giác vuông là: P = a + b + c Trong đó
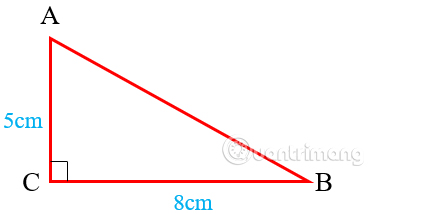
Ví dụ: Tính chu vi tam giác vuông với độ dài CA = 6cm, CB = 7cm và AB = 10cm. Dựa vào công thức tính chúng ta có cách tính P = 6 + 7 + 10 = 23cm. Ngoài ra chúng ta cũng có thể tính chu vi của tam giác vuông khi biết độ dài 2 cạnh. Cho tam giác vuông với chiều dài CA = 5cm, CB = 8cm, tính chu vi. Như hình dưới đây do tam giác vuông ở C nên cạnh huyền là AB. Để tính cạnh huyền tam giác vuông cân, ta sẽ dựa theo định lý Pitago trong tam giác vuông. AB² = CA² + CB² AB² = 25 + 64 AB = 9,4cm Vậy chu vi tam giác vuông CAB là: P = 5 + 8 + 9,4 = 22,4cm
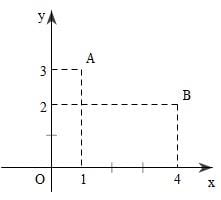
Giả sử bạn có bài toán cần tính chu vi tam giác trong không gian như sau: Bài toán: Trong không gian cho mặt phẳng Oxy, có hai điểm A(1;3), B(4;2). a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA=DB; b) Tính chu vi tam giác OAB? Tính chu vi tam giác trong không gian
Sau đây là lời giải của bài toán trên: Tính chu vi tam giác trong không gian
Tính chu vi tam giác trong không gian
Công thức tính đối với dãy số cách đều:
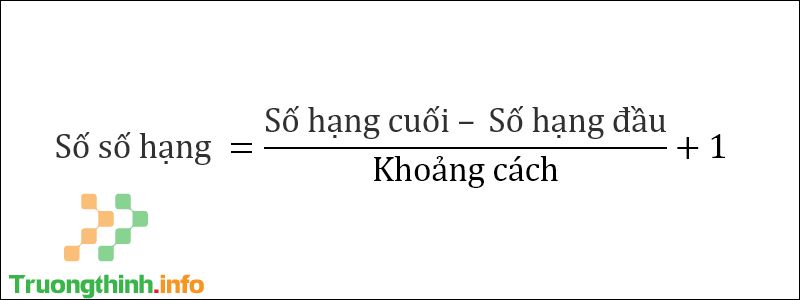
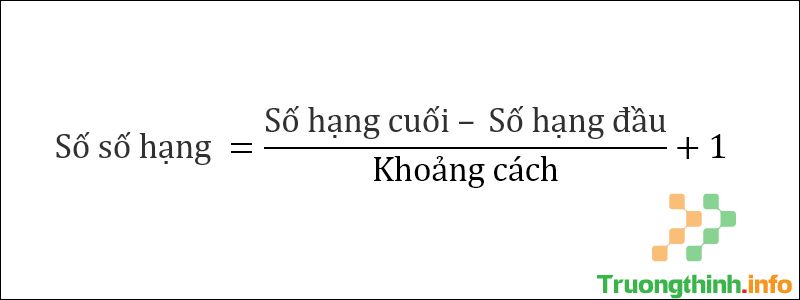
Công thức tính đối với dãy số cách đều Ngoài ra, dưới đây là công thức tính số số hạng cho một dãy số:
Công thức tính số số hạng cho 1 dãy số 3. Công thức tính tổng dãy số cách đềuCông thức tính tổng dãy số cách đều
Công thức tính tổng dãy số cách đều Tính số cuối cách đều
Công thức tính số cuối cách đều Tính số đầu cách đều
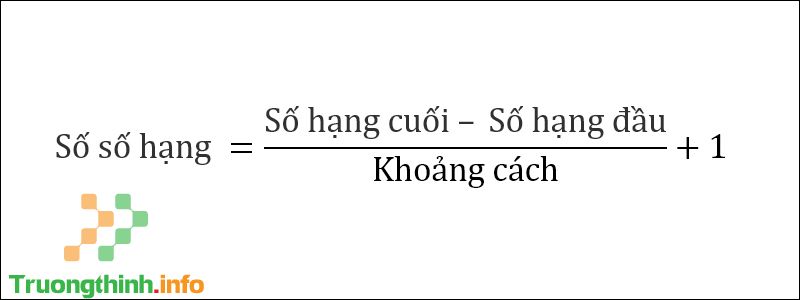
Công thức tính số đầu cách đều Tính số số hạng trong dãy
Công thức tính số số hạng trong dãy số cách đều Tính bình quân cộng
Công thức tính trung bình cộng của dãy số cách đều Mời bạn tham khảo bài viết Trung bình cộng là gì? Công thức và phương pháp tính bình quân cộng dễ dàng để tìm hiểu thêm nhé! 4. Cách giải bài toán tính tổng của dãy số có quy luật cách đềuBước 1 : Thực hiện tính số số hạng có trong dãy với công thức sau:
Công thức tính số số hạng có trong dãy cách đều Bước 2 : Áp dụng công thức tính tổng của dãy:
https://vio.edu.vn/ https://www.liveworksheets.com/worksheets/en https://www.tienganh123.com/tieng-anh-pho-thong https://ioe.vn/myioe https://www.youtube.com/ https://ieltsonlinetests.com/vi/ielts-exam-library#academic
thả like cho mình nếu câu hỏi ;câu trả lời và công thức hữu ích
Hình trụ tròn là hình có hai mặt đáy là hai hình tròn song song với nhau và bằng nhau. Ta có thể thấy rất nhiều hình trụ được sử dụng trong thực tế có thể kể đến như: lon sữa bò, cốc uống nước, lọ hoa, thùng đựng nước,… Hình trụ được sử dụng khá phổ biến trong thực tế do đó cách tính thể tích hình trụ cũng được áp dụng rất nhiều trong thực tế. Để có thể tính được thể tích hình trụ thì bài viết dưới đây là một trong những bài viết mà các em không nên bỏ qua.
Để tính thể tích khối trụ, ta lấy chiều cao nhân với bình phương độ dài của bán kính hình tròn ở mặt đáy hình trụ và số pi. V = π. r2. h
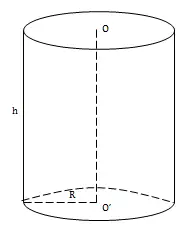 Khối trụ Trong đó: V là thể tích khối trụ có đơn vị là mét khối (m3) r là bán kính hình tròn ở mặt đáy khối trụ h là chiều cao của khối trụ π là hằng số pi ( π = 3, 14) BÀI TẬP VẬN DỤNGBài 1: Tính thể tích của khối trụ biết khoảng cách giữa hai tâm đáy là a (cm) và đường kính của đáy là b(cm)
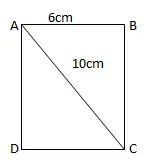
Bài 2: Cho hình chữ nhật ABCD có AC = 10cm, AB=6cm. Cho đường gấp khúc ABCD quay quanh AD ta được 1 hình trụ. Tính thể tích khối trụ được giới hạn bởi hình trụ trên.
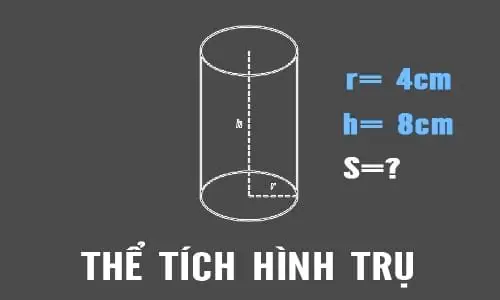
Bài 3: Cho một hình trụ bất kỳ có bán kính mặt đáy r = 4 cm , trong khi đó, chiều cao nối từ đỉnh của hình trụ xuống đáy hình trụ có độ dài h = 8 cm . Hỏi thể tích của hình trụ này bằng bao nhiêu ?
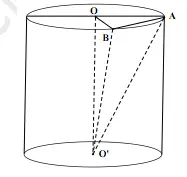
Bài giải: Bán kính mặt đáy hình trụ r = 4cm, chiều cao hình trụ h = 8cm. Áp dụng công thức tính thể tích hình trụ ta được kết quả như sau: V = π x r2 x h = π x 42 x 8 = ~ 402 cm3 Bài 4: Cho hình trụ có đáy là hai hình tròn tâm O và O’, bán kính đáy bằng 2. Trên đường tròn đáy tâm O lấy dây cung AB=2. Biết rằng thể tích khối tứ diện OO’AB là 8. Tính thể tích khối trụ. Giải:
Tam giác OAB có OA = OB = AB = 2 SOAB = Tam giác OAB có OA = OB và OO’ vuông góc với (OAB) Suy ra OO’
Vậy thể tích hình trụ là:
Bài 5: Cho hình trụ có bán kính đáy x, chiều cao y, diện tích toàn phần bằng . Với giá trị x nào thì hình trụ tồn tại ? Tính thể tích V của khối trụ theo x và tìm giá trị lớn nhất của V Đáp án: hình trụ tồn tại khi 0 < x < 1
Bài 6: Bên trong hình trụ có một hình vuông ABCD cạnh a nối tiếp mà A, B thuộc đường tròn đáy thứ nhất và C, D thuộc đường tròn đáy thứ 2 của hình trụ, mặt phẳng hình vuông tạo với đáy hình trụ một góc 450. Tính thể tích khối trụ
Bài 7: Cho một hình lăng trụ đứng ABCA1B1C1 có ABC là tam giác vuông. AB = AC = a; AA1 = a . M là trung điểm AA1 . Tính thể tích hình lăng trụ MA1BC1
Bài 8: Cho hình lăng trụ ABCA’B’C’ có đáy là tam giác đều cạnh a, cạnh bên AA’ = b. Tam giác BAC’ và tam giác B’AC là các tam giác vuông tại A a) Chứng minh rằng: Nếu H là trọng tâm của tam giác A’B’C’ thì AH vuông góc với (A’B’C’) b) Tính VABCA’B’C’ Đáp án
Bài 9: Cho hình trụ có đáy là đường tròn tâm O và O’ tứ giác ABCD là hình vuông nội tiếp trong đường tròn tâm O, AA’, BB’ là các đường sinh của khối trụ. Biết góc của mặt phẳng (A’B’CD) và đáy hình trụ bằng 600 . Tính thể tích khối trụ Đáp số:
Bài 10: Một hình trụ có diện tích toàn phần Đáp số: Vmax khi R = 1, h = 2 Bài 11: Cho hình trụ có 2 đáy là 2 đường tròn tâm O và O’, bán kính đáy bằng r, chiều cao bằng h. Hai điểm A, B lần lượt thay đổi trên 2 đường tròn đáy sao cho độ dài AB = d không đổi (d>h). a) Tính thể tích của tứ diện OO’AB theo r, h, d. b) Chứng minh rằng: khoảng cách giữa 2 đường thẳng AB và OO’ không đổi Bài 12: Cho hình lăng trụ ABCA’B’C’ có độ dài cạnh bên bằng 2a, tam giác ABC là tam giác vuông tại A, AB = a, Đáp án: VA’ABC = a3 / 2
1. Soạn bài không phụ thuộc vào sách tham khảo 2. Đọc sách nhiều 3. Luyện viết nhiều để học tốt hơn 4. Nắm vững chắc kiến thức . -Nắm chắc kiến thức mới học tốt môn Ngữ Văn lớp 6 -Muốn học tốt môn Ngữ Văn lớp 6 cần phải luyện viết nhiều -Tìm trung tâm ôn luyện văn hóa
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Trang chủ
Giải bài tập Online
Flashcard - Học & Chơi
Dịch thuật
Cộng đồng
Trắc nghiệm tri thức
Khảo sát ý kiến
Hỏi đáp tổng hợp
Đố vui
Đuổi hình bắt chữ
Quà tặng và trang trí
Truyện
Thơ văn danh ngôn
Xem lịch
Ca dao tục ngữ
Xem ảnh
Bản tin hướng nghiệp
Chia sẻ hàng ngày
Bảng xếp hạng
Bảng Huy hiệu
LIVE trực tuyến
Đề thi, kiểm tra, tài liệu học tập





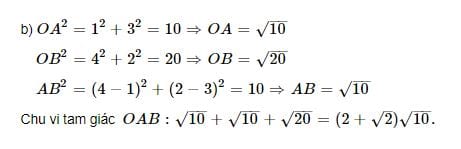
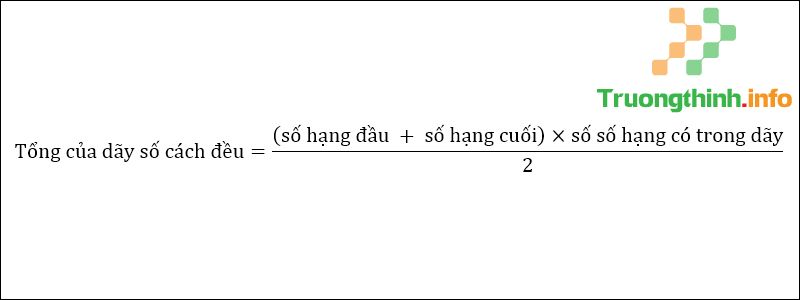
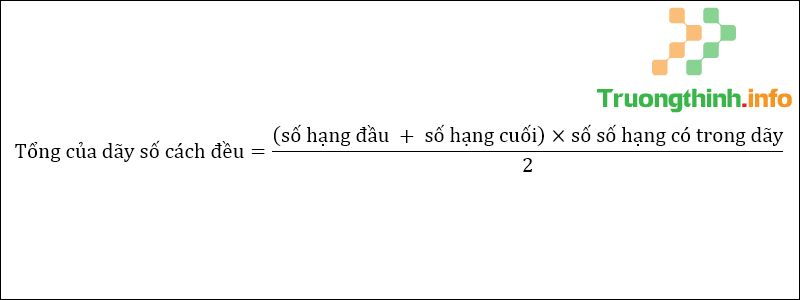



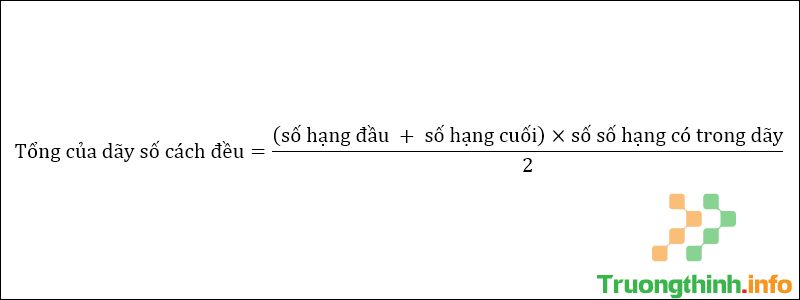





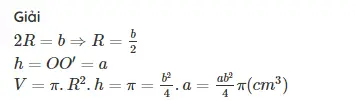
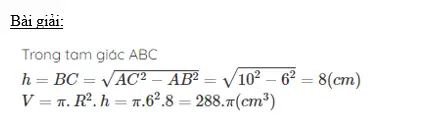
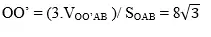
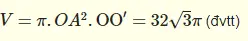
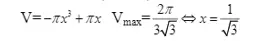
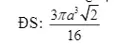
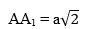
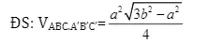
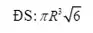
 . Xác định các kích thước của khối trụ để thể tích của khối trụ này lớn nhất
. Xác định các kích thước của khối trụ để thể tích của khối trụ này lớn nhất
